
It’s actually already almost one year since I finished the work on an Erasmus project in Universitat Politècnica de València, Spain. The goal was to speed up the computation of distance estimated 3d fractals in a way so that they could be computed in real time and therefore make it possible to explore them in an interactive fly through program.
Fractals are graphics produced by recursive mathematical formulas. Sine the graphics are purely based on math, one can zoom in infinitely into them without loosing quality, well – as long as the float precision is enough. One classical 2d fractal is the Mandelbrot. Some years ago a formula for a 3d Fractal was found that resembles a Mandelbrot and the structure was called Mandelbulb.
Although there already exist programs that do the fractal computation on the graphics card, none of the ones I found was able to do it in acceptable quality and real time. Some of them produced nicer images, but at the cost of having long rendering times, others where sort of interactive, but the quality was bad.
I first implemented a quick proof of concept using NVIDIA OptiX, based on their Julia example, but OptiX quickly showed its limitations, especially when I started to work on a method to speed the thing up. So I switched to NVIDIA CUDA and was satisfied with that decision (and anyway, as I will blog soon, I recommend to stay away from OptiX as far as possible : ).
I’ll explain in a few sentences how the rendering works, details for the traditional method can be found on the page of Mikael Hvidtfeldt Christensen and for both, the traditional and improved one in my report linked below.
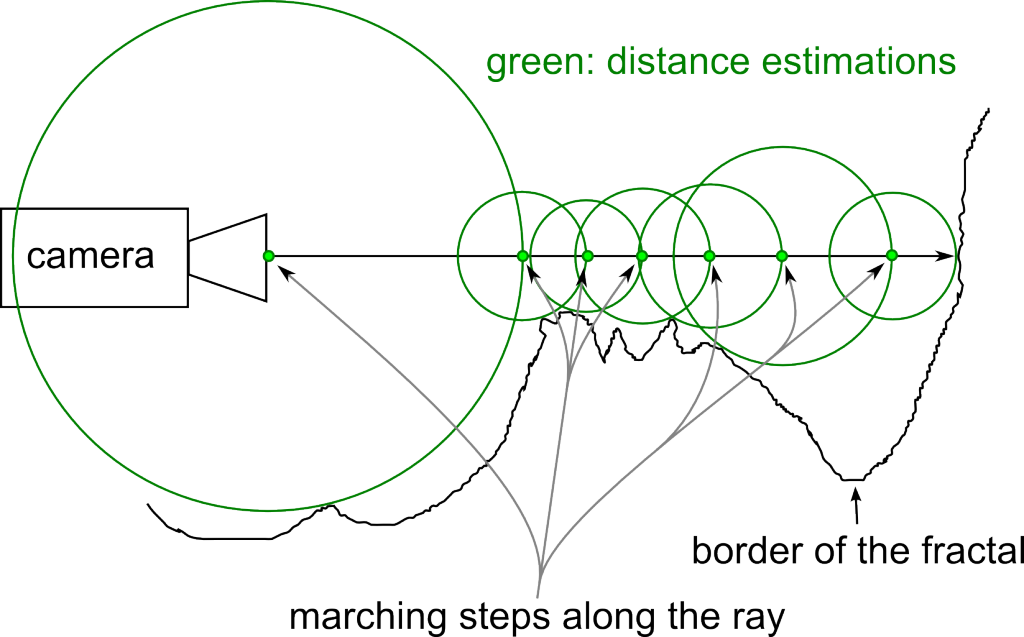
There is a function, which returns the maximum lower bound for the distance to the fractal, called the distance estimator (DE). When walking along a ray, for instance shot by the camera, it is safe to walk this distance, because we have the guarantee that the fractal won’t intersect the ray in this interval. After one step, the distance is estimated again and we march as long, as the estimated distance is above a certain threshold.
My idea to speed up the rendering was to decrease the amount of computation by letting neighbouring rays “ride” on the previous rays.
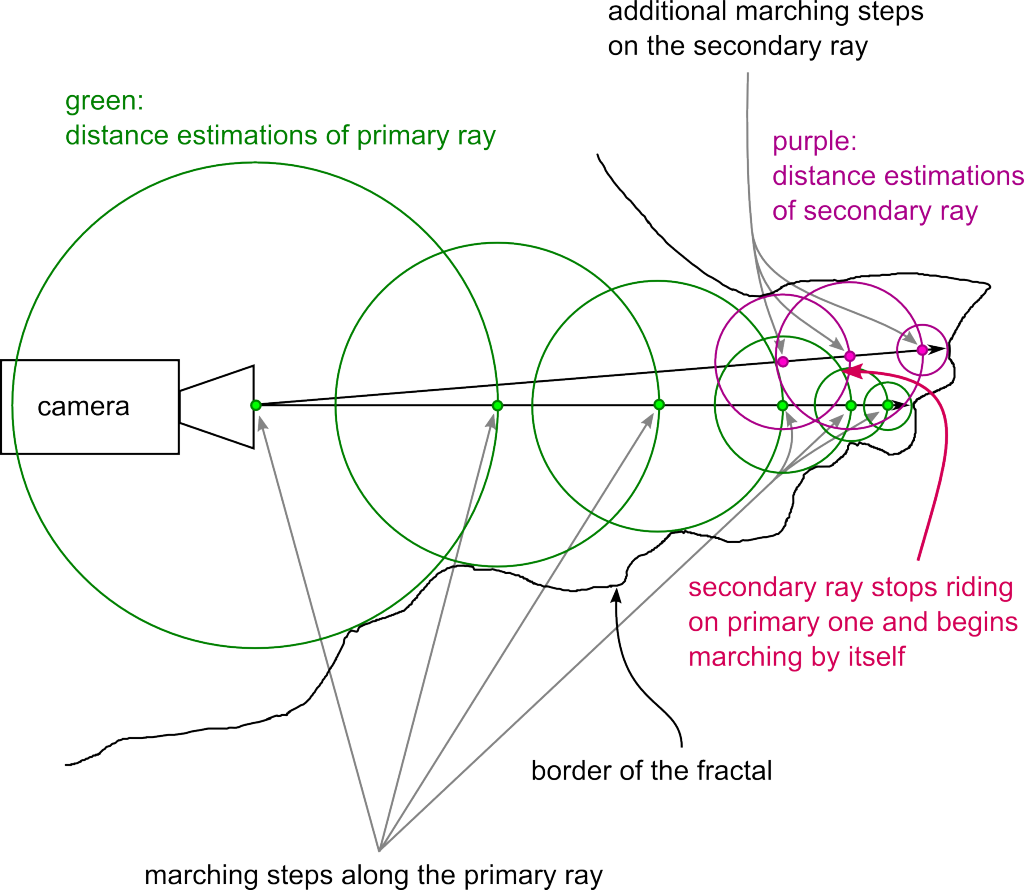
This works in two passes, first, “primary” rays are shot with a distance of several pixels to each other, recording the DE values. Secondly, the neighbours, called secondary rays in the figure, are shot. Those can use the information calculated in the first pass to jump straight to the end of the stepping. So, that’s it, in short. Don’t confuse the terms primary and secondary rays with bouncing light of ray tracing here.

Comparing the traditional ray marching algorithm with the new, faster one, shows a speed up of up to 100% and interactive exploration in almost all views without shadows. It would be probably possible to also implement this speed up for shadow rays, but I had no time to do it. Unfortunately there are some artefacts due to the ray “riding”, details can be found in the report. If you are interested into the source code, please write me a message.
Edit: The reason I don’t publish the repository is that there is still some (c) NVIDIA code inside (setting up CUDA, the render window etc). If there is somebody willing to replace / redo that code with something GPLv3, check the build and maybe update to the newest sdk, that would be most welcome :)
Edit2: Ok, the GPL parts of the source code are published now. I’m aware that it does not compile, however I haven’t got the time to replace the NVidia parts taken from the examples. Maybe it’ll help some of you anyways :)

Hello! Congrats for the software! I am really interested into the source code, because I’m passionate about Julia & Mandelbrot sets, but I would like to start studying Mandelbulb, too.
Hi,
I’ll send you an email in the evening..
Edit: Done
Cheers..
Adam, I would be very interested in seeing your code for this. I am currently working on a project that requires CUDA (for medical imaging) but I am also a big fan of the Mandelbrot set and fractals in general. In fact, I have developed a whole cosmology based fractal theory. Please let me know if it is possible to see your code. It would be a great help to me. Thanks.
Lori Gardi aka FractalWoman
sure, check your mail..
Hi Adam,
I’ve read your detailed report and very interested in seeing your code. Can I have your code so that I can study your implementation?
Thanks
Check your mail :)
Hello.
It’s an interesting project! Can I see your code, please?
Check your mail..
cheers
Hy Adam, I too would really like to see your code :)
Cheers Julian
Sorry for the delay. I have many things on my plate right now and this website is just not on top of the priority list :)
I’ve sent you an invitation to the repository. Keep in mind that some of the code is (c) NVIDIA and you are not allowed to make it public (it’s from the CUDA examples). My own code you can licence GPLv3.
cheers, Adam
Hi Adam,
Can I see source as well? I am learning Vulkan API and think it would be an interesting exercise to write a mandelbulb viewer.
Thanks!
Hi, I’ve edited the post to include the non proprietary code. Hope it helps.
Cheers, Adam
where can we download the windows exe of the cuda version ? thanks
I’m sorry, but there is none. Back then I’ve built it on linux and not even these binaries are available any more. I fear that all this won’t be useful to you unless you are a programmer :)
Cheers, Adam